Jump to content
Banner by ~ Discord The Overlord
Guidelines

Astralshy

Support
 View Profile  See their content

  • Posts

    3,762

  • Joined

  • Last visited

  • Days Won

    88

 Content Type 

Posts posted by Astralshy

    hi theree

    in Welcome Plaza

    Hello and welcome @Millielovesyou,

    I hope you have a great time here and find many new great friends :>

    It is also so nice to meet you ♥

     

    And no worries it is not out of the norm :> Just the opposite it is appreciated for you formally introducing yourself to the community

    If you have any question feel free to ask ♥

    • Brohoof 2

    Problem #1

    in Problems

    It has been a while, I'm more applied maths guy and less proofing. But let's see if I can still do this :>

    Spoiler

    Let's put down what we know from the problem

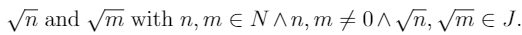    image.png    (1)

     

    Let's try proof by contradiction on this, so let's assume such roots would add up to a rational number p/q

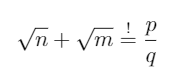    image.png     (2)

    With p, q in Z and q ≠ 0

    Any fraction/rational number you can split up in two smaller fraction which would add up the original fraction, like this

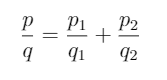    image.png    (3)

    with of course

    image.png    (4)

     

    let's define these two new variables δ, ε regarding the difference of these fractions and those roots

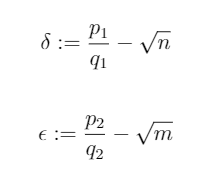    image.png    (5)

    Now let's think: δ, ε must be both unequal to zero. Because if these would be zero then square roots of n and m would be both rational numbers and would contradict the problem.

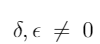    image.png     (6)

    Now let's add these two equations/ definitions together

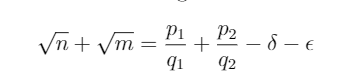    image.png    (7)

    since all these fractions p_i/q_i are the same, we can use the earlier equation and add the sub fraction together to the original one

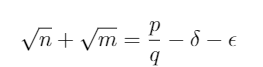    image.png    (8)

    and this contradicts 1, since δ, ε ≠ 0.

    Or in simple words: either  those roots of n and m are both rational numbers (δ, ε = 0) or they dont add up to a rational number (δ, ε ≠ 0).  When both conditions are applied then this leads to the contradiction of δ, ε = 0 and δ, ε ≠ 0 at the same time

    So, disproved which means two rational numbers don't add up to a rational number

     My thoughts

    I think this proof is a bit too unspecific to your problem/ I think there maybe a more direct one since this is very general way

    This proof relies on the proof that a irrational number cannot be written as a fraction with p/q with p,q in Z and q unequal to 0. So I had the feeling while reading the problem that some things are known.

    • Brohoof 1

    Oreos

    in General Discussion

    Famous Oreos cookies

    Really good cookies. They are not so common here as as in America, so I hope you can forgive me for not having seen/tasted all those variations you are accustom to.

    So I say I like the normal ones :> I'm very boring and eat them in a  very boring cookie-monster-way *nomnom

     

    • Brohoof 1
×
×
  • Create New...