-1/12
Some time ago there was some controversy across the Internet whether 1+2+3+4+... = -1/12 or not. Here's what I think about this:
Clearly, this sum diverges to infinity, so you can't assign any finite value to it, using the standard math rules. But there is a way to associate this value with this sum, which uses some advanced concepts that I don't fully understand, like analytic continuation, Riemann zeta function, and Ramanujan summation.
So I did something different. First, I took the formula for partial sums: S(n) = n * (n -1) / 2, and treated is as a function of all real numbers: f(x) = x * (x -1) / 2. It's a quadratic function, with a graph that looks like this:
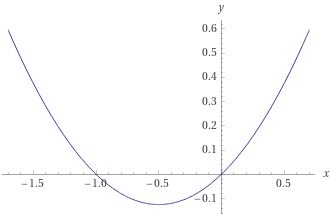
Between -1 and 0 the value is negative. I wanted to know the area between the x axis and function in that interval, so I took the integral. And guess what? The result is -1/12. Coincidence? I think not.
Later I watched this video, and it confirmed my suspicions that something interesting is going on here. It's in the last minute of the video.
Edited by Silly Druid
-
 3
3



9 Comments
Recommended Comments
Create an account or sign in to comment
You need to be a member in order to leave a comment
Create an account
Sign up for a new account in our community. It's easy!
Join the herd!Sign in
Already have an account? Sign in here.
Sign In Now